在能源系统的优化中,一个新的决策必须考虑到系统当前的状态,因为当前的状态又受上个时间段决策的影响,所以一个新的决策实际上也取决于上个时间段的控制决策,这种决策问题成为多阶段决策问题。美国学者贝尔曼(R.E.Bellman)为解决非线性动态系统多级决策的控制问题,提出了动态规划方法,其核心是贝尔曼最优原理。这个原理是把一个多步决策问题转化为多个一步决策问题,从而简化了求解过程。从本质上来说,强化学习算法和模型预测优化算法都只是贝尔曼优化原理的某个具体应用。
从大的方面分类,强化学习算法可以分为四类,基于模型的间接生成策略算法,基于无模型的间接生成策略算法,基于模型的直接生成策略算法,基于无模型的直接生成策略算法。有无模型的算法区别在于有模型的算法需要提前构建环境(系统)的动态模型,而无模型的算法则无需。间接生成策略的算法依靠不断迭代评价函数生成最后的策略,而直接的算法则直接以求解策略或策略函数对应的参数作为目标。以下对各类算法取几种常用的算法进行介绍。
表1. 强化学习算法分类
|
基于模型算法 |
无模型算法 |
| 间接生成策略 |
ADP |
MC, Q-learning, DQN |
| 直接生成策略 |
PILCO |
DDPG |
1. 基于模型的间接生成策略算法
1.1 动态规划(DP)算法
DP是整个强化学习理论重要的基础,从过程上看,它可以分为策略评估与策略改进两个部分,前者为后者之前提。策略评估涉及对某一个固定不变策略的评价:使用某一个固定的策略在系统中交互,根据反馈信号计算该策略的好坏。策略改进是对某一个策略进行改进的操作:根据对策略的评价,将该策略的某一个动作或某一部分替换为更好的动作。反复进行以上两部操作,策略将收敛到一个不变的最优策略上,整个过程被称为策略迭代。根据不同的迭代形式又有值迭代、异步迭代算法等。
1.2 自适应动态规划(ADP)算法
ADP在动态系统的相关方程未知的情况下,通过自身建立一个动态系统模型来近似地求解动态规划问题。此外,ADP也利用函数近似结构逼近动态规划方程中的性能指标函数(评价网络)和控制策略(动作网络),一般包括三个部分:动态系统,评价环节,和执行环节,每个部分均可由神经网络代替。其中动态系统对应于建立的系统模型,执行环节寻找最优控制策略,评价环节基于贝尔曼原理对执行环节的参数进行动态更新。下图为一种ADP算法的示意图。
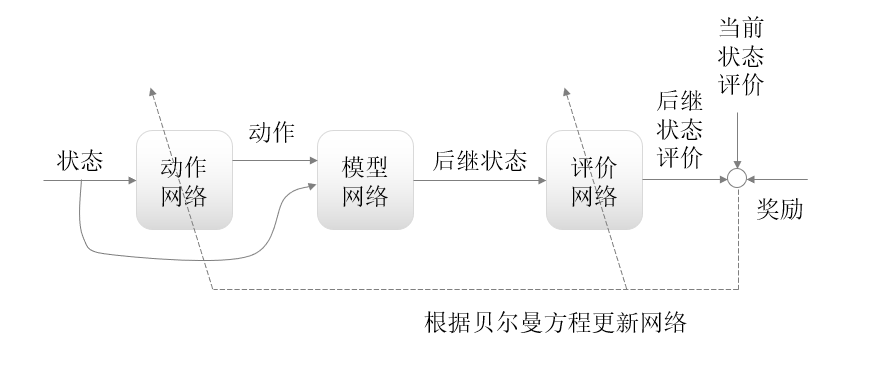
图1. 动态规划原理
2. 基于无模型的间接生成策略算法
2.1 蒙特卡洛(MC)算法
同样对于系统动态未知的情况,MC无需建立系统的模型,而是通过不断采样生成轨迹,再根据其中的样本生成自己的评价函数。在强化学习算法中,为了避免优化结果陷入局部最优,而无法生成更多样的轨迹,往往会采取近似贪心算法。即以1-ε的概率选择当前最优动作,以ε的概率从所有动作中均匀随机选取。采用近似贪心策略之后,当前最优动作被选中的概率是1-ε+ ε/A,非最优动作被选中的概率是ε/A。每个动作都有可能被选取,而多次采样将会产生不同的采样轨迹。MC算法的一次更新往往发生在一个轨迹采样结束后(或者说,一个情节结束后),因为对所有状态或者动作的评价都需要用到被评价时间点后所有的反馈。该次更新会使轨迹中所有样本中出现的状态或者动作的评价进行重新计算。
下面的算法展示了一种MC的实际操作过程,其通过评价动作进而生成控制策略(最后两行)。在外循环中,对于每个情节,为了尽可能地探索到更多地状态-动作对,应使所有的被选概率都大于0,一种常用的方法即近似贪心算法。在一个情节完成后,即进入内循坏,对其中所出现的所有状态-动作对进行估计,即评价。

2.2 Q-learning与DQN算法
为了提高更新的频率,Q-learning在每次搜集到一个样本后就对相应的动作进行一次评价的更新,而不是像MC那样需要等到一个轨迹完全生成,这样的方法也被称为时间差分法(TD)。强化学习算法Q-learning与DQN的学习原理类似,核心都是通过Q值来进行决策与更新,在每一个状态下,在带有一定随机概率的决策过程中选取该状态下Q值最高的动作,进而执行该动作得到环境在执行动作后的反馈,并学习反馈的经验后更新Q值,最后进入下一个状态,进入循环。以下是相对应的算法步骤,对比MC算法可以明显看出,两者的最大区别在于Q-learning利用了下一个状态的最优估计值来估计当前状态-动作对,而不是像MC中使用真实的反馈累计。

DQN最主要的特点是提供了人工神经网络来近似动作值函数(Q函数)。DQN和Q-learning的区别是Q-learning采用Q表来记录不同状态与动作下的Q值,决策时通过查询Q表中对应状态下Q值最高的动作进行决策,更新即通过状态与动作获取的反馈来更新表格中的Q值;而DQN采用神经网络来拟合Q表,决策时通过神经网络得到不同动作下的Q值,选取Q值最大的动作,更新即更新整个神经网络。因此采用了神经网络的DQN在复杂场景下有着更好的性能与更快的收敛速度。
可以发现,如何选取两个算法的重点在于判断整个控制任务是否是复杂场景。具体地,当状态空间和动作空间在整个问题的设定中本身就是离散的,那么此时Q-learning可能更具有优势;当状态空间是连续的时,一种方法仍是使用Q-learning,但需要先离散化状态空间,离散化的操作可以是一般定距的离散化,也可以是加入专家经验等不规则的划分,如果此时Q-learning的效果不佳,就应考虑使用DQN来尝试该场景。
因为强化学习不像大多数深度学习一样,样本不是独立同分布的(之前的动作将影响之后样本的概率,样本的分布也随策略的变化而改变),所以在拟合网络时,DQN提出了经验回放(Experience Replay, 2013NIP版)和目标网络(2015Nature版),前者将样本放到经验池中反复使用来减弱样本之间关联性,后者用新增的目标网络的估计值来更新原来的网络将顶目标网络的更新频率来增加训练的稳定性。
3. 基于模型的直接生成策略算法
3.1 PILCO算法
Probabilistic inference for Learning Control(PILCO)算法是一个基于高斯概率模型进行推理和优化的算法。这个算法基于三个层次的工作,在底层学习一个状态转移的概率模型,在中间层对策略pi下的值函数V进行策略评估,最后在顶层对策略pi进行参数更新。作为一个基于模型的算法,与其他算法最大的不同是,PILCO在对系统动态建模时,不只是在建立一个固定的近似模型,而是建立一个概率动态模型,即多个模型上的分布。
此外,在PILCO算法还有两个特殊之处,第一个用高斯概率模型预测下一步的状态,第二个PILCO算法没有强制从状态空间到动作空间的策略,该策略可以由使用者自己定义,并根据第三层次的评估对策略参数进行优化。
4. 基于无模型的直接生成策略算法
4.1 DDPG算法
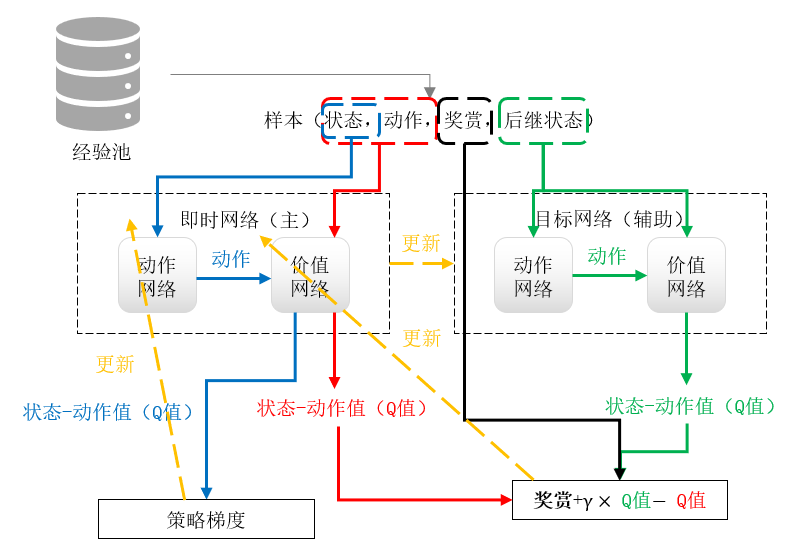
深度确定性策略梯度(Deep Deterministic Policy Gradient)算法采用策略梯度解决了DQN网络不能处理连续动作空间的问题。该算法包括了四个网络,动作目标网络,动作即时网络,价值目标网络,和价值即时网络。在该算法中,价值即时网络负责逼近真实的反馈,动作即时网络作为策略函数输出相应的动作并向最优策略逼近。目标网络作为辅助网络将协助价值即时网络的更新来逼近真实反馈,在即时网络内部实现类似actor-critic算法的更新:由价值即时网络协助动作网络更新。目标网络的参数由即时网络的参数以一定学习率更新。以下为DDPG整个训练的示意图。