以下来自国际期刊Energy&Buildings的论文,如有需要,请引用 S.Qiu, Z. Li, Z.Li*, et al., Model-free control method based on reinforcement learning for building cooling water systems: Validation by measured data-based simulation, Energy and Buildings 218 (2020) 110055.
摘要
在建筑空调系统的优化控制中,基于模型的预测控制方法(MPC)是广为研究和使用的方法。然而,MPC方法需要系统的传感器较为全面和准确,这一点在实际项目中往往很难满足。为了解决这个问题,本文提出了一种基于强化学习的无模型优化方法,并将其用于空调冷却水系统的优化。在该方法中,状态变量是湿球温度和系统冷负荷,动作变量是风机和水泵的频率,优化目标是系统效率COP. 在某基于实际数据搭建的模拟环境中,该方法与局部反馈控制、模型优化控制进行了对比。结果表明,与固定参数的控制策略相比较,无模型优化可以节约能耗11%,高于局部反馈控制的7%,但低于模型预测控制的14%。结果表明,三个月的训练数据足以让无模型优化方法达到比较好的节能效果。
方法介绍
2.1 方法概述
Q-learning是一种基于Q表的强化学习算法,与基于神经网络的深度强化学习算法相比,该方法较简单且易收敛,因而在工程应用中具有更强大的生命力。
2.1.1 优化目标
本文的优化目标是系统效率,该效率可以通过以下公式计算求得。
COP = CL/(Ech+Epump+Etower)
在上式中,CL表示冷负荷,Ech,Epump,Etower分别表示冷水机组、冷却水泵和冷却塔的功率。
2.1.2优化变量
本文中的优化变量是冷却泵和冷却塔的频率。
2.1.3 优化需要已知的前提条件
本方法需要已知系统的连接方式、历史的气象数据、以及设备的名义参数表。本方法不需要建模型,但需要采集三个方面的信息: 设备的功率信息,设备的开关和频率信息,以及系统的负荷信息。
2.1.4 优化间隔
由于两个方面的原因,优化的时间间隔应当设置在20分钟到60分钟之间。第一,完全没有经过训练的强化学习控制器会输出随机策略,当间隔时间很短时系统会出现波动性,第二,强化学习控制器需要较为准确的环境反馈,只有当经过足够长的时间之后,系统稳定后的表现才能够用来准确地评估动作的效果。
2.1.5 优化流程
本文提出的优化流程如下图所示,共包括六个步骤。第一步,依据系统的启停策略计算各类设备的开关状态;第二步,对湿球温度和系统冷负荷进行离散,以匹配Q表的结构;第三步,对冷却塔风机的频率基于Q-learning方法进行优化,首先找到Q-表中当前状态对应的最大值,然后对Q表中上个状态对应的Q值进行更新,最后基于优化策略决定最优频率;第四步,使用同样的步骤对冷却水泵的频率进行优化;第五步,将各设备的开关状态及频率信号下发到设备,第六步,记录下当前的状态,作为下个时间步长的上个状态值。

图1. 无模型优化流程
2.2 启停控制策略
本文通过如下启停控制策略决定设备的启停信号:
(1) 如果负荷低于单台冷机名义制冷量的50%,所有冷机都不开
(2) 当冷机开的时候,所有冷却塔都保持常开
(3) 根据冷负荷的大小判断开启冷机的台数。当冷负荷大于单台冷机制冷量的105%时,再开启一台冷机;
(4) 冷却水泵和冷冻水泵的开关与冷机联动。当冷机开启时,先开启对应的冷却水泵和冷冻水泵
(5) 冷冻水泵的频率维持在工频
(6) 冷机出水温度设定在名义出水温度
2.3 Q表的配置和初始化
本文中,冷却泵和冷却塔的优化各设置一个独立的智能体,每个智能体都有一个独立的Q表,该Q表的形式如下图所示。表格中的列表示不同的状态组合(湿球温度与冷负荷的组合), 行表示不同的动作,对于冷却泵智能体,就是冷却泵的频率,对于冷却塔智能体,就是冷却塔的频率。
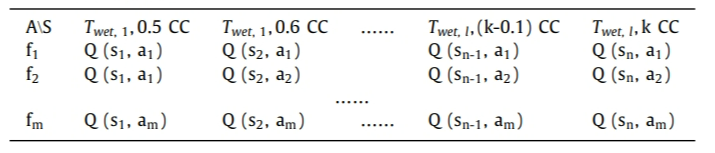
图2 Q表的形式
2.3.1 状态
本文中,由于三个原因,将状态定义为湿球温度和负荷的组合。第一,系统的控制动作不能够改变湿球温度和冷负荷;第二,系统冷负荷是影响系统效率的重要因素之一;第三,湿球温度对于冷却塔的制冷能力及整个系统的效率具有重要的影响。
两个状态变量按如下方式进行离散。第一,湿球温度按每1℃进行离散,上下限由该城市的历史气象数据决定;第二,系统冷负荷按照单台冷机最大制冷量的10%进行离散,如果某系统有k台相同冷量的冷机,离散后的冷负荷可以表达为0.1CC, 0.2CC,...,k CC。两个状态变量的所有组合构成了整个优化问题的状态空间。
2.3.2 奖赏
本文将系统效率作为优化目标,及奖赏。
2.3.3 动作
本文将冷却水泵和冷却塔的频率作为控制动作。应当注意到,不同的动作需要规定一个安全运行的边界,以保持设备的正常运行。比如,一般水泵的频率不会低于
20 Hz.本文频率控制的精度是1Hz.
本文中,状态和动作的离散精度的设定是基于探索时间以及传感器精度的考虑。更高的传感器精度可以带来更高的离散精度,但离散精度的提高会扩大Q表的规模,在提升节能效果的同时显著延长学习时间。
2.4 决策和Q表更新
一般而言,Q表按照贝尔曼原理进行更新,如下式所示。
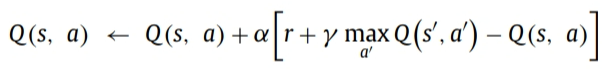
其中Q(s,a)表示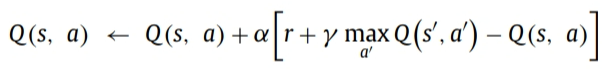 上个状态和动作对应的Q值,r表示上个动作得到的奖赏,α表示学习率,学习率越高,Q表更新的速度越快,本文取0.9,γ表示未来的状态对于当前动作的影响。由于当前的动作不会影响下个时刻的状态,因此可以不需要考虑该影响因素。本文中取0.05.
上个状态和动作对应的Q值,r表示上个动作得到的奖赏,α表示学习率,学习率越高,Q表更新的速度越快,本文取0.9,γ表示未来的状态对于当前动作的影响。由于当前的动作不会影响下个时刻的状态,因此可以不需要考虑该影响因素。本文中取0.05.
在Q表更新完之后,需要根据当前的表格做控制动作的决策。一般的决策算法是近似贪婪算法,如下式所示。
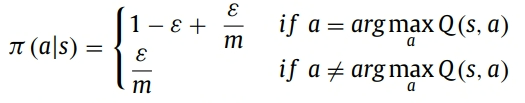
式中ε是预先定好的概率参数,代表探索的可能性。该值越小,代表越有可能从当前的Q表中选择最优策略,反之,该值越大代表算法越有可能随机探索一个可能的动作。因此ε是一个大于0,小于1的数。m是当前状态下所有可能的动作的数量。π(s,a)代表在当前状态s下,选择动作a的概率。